搜索与图论2.1

本节主要介绍一下 \(Dijkstra\) 算法。该算法主要用于解决单源最短路问题，且该问题中的边权不为负数。

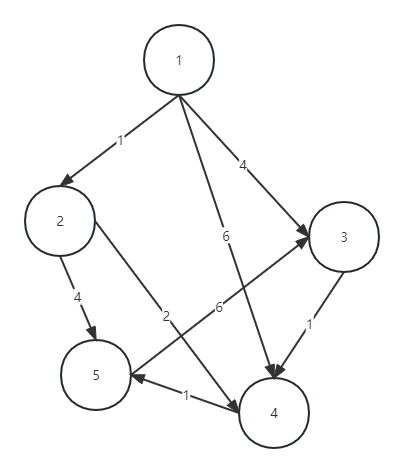基本思想：我们假定有一张没有负权的图，该图如下 \(dist\) 数组的元素 \(dist[i]\) 表示从起点到 \(i\) 的距离，初始化为正无穷。假设起点为 \(1\)，那么 \(dist[1]=0\)。然后我们迭代 \(4\) 次。首先我们找到不在集合 \(S\) 中且其距离起点最近的点 \(t\)，将 \(t\) 并入 \(S\) 中，用 \(t\) 来更新到其余点的距离。参考样图，\(dist[1]=0\)，而其余的 \(dist\) 均为正无穷，那么先找到的是 \(1\)，将 \(1\) 并入 \(S\)，对于可以由 \(1\) 的所有出边的点的距离进行松弛，我们可以得到 \(dist[2]=1,dist[3]=4,dist[4]=6\)。然后我们对于不在集合 \(S\) 中且距离起点最近的点为 \(2\)，我们将 \(2\) 并入 \(S\)，对于 \(2\) 的所有出边的点的距离进行松弛，也就是 \(dist[4]=3,dist[5]=5\)。然后就考虑 \(4\)，加入集合 \(S\)，进行松弛。直至所有的点都加入 \(S\)。

对于数据范围较小，且为稠密图的可以使用邻接矩阵进行图的存储，该算法朴素版的时间复杂度为 \(O(n^2)\)。而数据范围大，稀疏图使用邻接表存储，并使用小根堆进行优化，时间复杂度为 \(O(mlogn)\)。

给定一个 \(n\) 个点 \(m\) 条边的有向图，图中可能存在重边和自环，所有边权均为正值。

请你求出 \(1\) 号点到 \(n\) 号点的最短距离，如果无法从 \(1\) 号点走到 \(n\) 号点，则输出 \(−1\)。

第一行包含整数 \(n\) 和 \(m\)。

接下来 \(m\) 行每行包含三个整数 \(x,y,z\)，表示存在一条从点 \(x\) 到点 \(y\) 的有向边，边长为 \(z\)。

输出一个整数，表示 \(1\) 号点到 \(n\) 号点的最短距离。

如果路径不存在，则输出 \(−1\)。

\(1≤n≤500,\) \(1≤m≤10^5,\) 图中涉及边长均不超过 \(10000\)。